Forge Has Got My Goat
Solving a children’s puzzle with and without temporal logic.
Forge is a hot new model finder heavily based on a previous tool, Alloy. Forge builds upon Alloy in several ways, one of which is the addition of multiple language modes. In this post, I describe Forge and its novel language modes. I pose a fun puzzle and solve it using two of Forge’s language modes. Finally, I contrast the two solutions using the different expressive constructs afforded by each mode.
The Tool:
For the uninitiated, model finding is a method for finding all counterexamples to a system specification (usually hardware or software) within some bounds. In this case, counterexample means any event that would violate a program specification. This means that a model finder will guarantee that particular properties will always hold for the system within some bounds. Or it will provide every way that those properties are violated (counterexamples) within the specified bounds. For example, a specification for a banking protocol may require that a bank transaction must be approved by both parties and terminated within two steps. If this specification is fed to Forge and the bounds are set to check all instances up to three steps, Forge will find any bugs in the banking protocol. In our case, we will write the constraints of a kid’s puzzle; the model finder will automatically find every possible solution to our puzzle for us.
Forge’s automated example finding makes it simpler to use than other formal methods software. The Forge model finder is unique in this area because it is built for formal methods pedagogy but remains advanced enough for modeling real-world problems. Forge is used in Computer Science courses at Brown University and the University of Utah.
Built with pedagogy in mind, Forge must be accessible for beginners to learn but have enough expressive power to remain helpful for real-world models. Forge achieves this by having three user modes: Froglet, Relational Forge, and Temporal Forge.
- Froglet: the simplest mode, providing logical quantifiers (e.g.,
someandall), partial and total functions, and little else - Relational Forge: allows all valid Froglet and arbitrary relations (e.g., set union, set difference, and transitive reflexive closure)
- Temporal Forge: builds on the two previous modes by allowing LTL operators to express models in the temporal domain
Although Froglet seems expressively destitute, particularly when compared to Temporal Forge, much of what can be expressed in Temporal Forge can also be expressed in Froglet. Building up these more complicated structures from a simpler initial language requires patience. But just how close is the expressive power of these two languages? What follows will be a first-step approach to the expressivity comparison between the simplest mode, Froglet, and the most complex mode, Temporal Forge.
The dedicated reader will notice that I have left out the middle child, Relational Forge. Unfortunately, arbitrary set relations cannot be used in the specification of the puzzle I have chosen for this post. Therefore, the specification of this puzzle would be the same in Froglet as in Relational Forge.
The Puzzle:
Instead of modeling a large-scale software system to keep things simple, I use a fun puzzle: Goats and Wolves. The puzzle takes several steps to solve, meaning that Temporal Forge’s extra operators will be handy (but aren’t strictly necessary). This reveals notable differences between the two language modes. The puzzle is as follows:
Three goats and three wolves want to cross a river. They have one boat, which can hold up to two animals.
- Initially, all six animals and the boat are on the near side of the river.
- At the end, all six animals and the boat must be on the far side of the river.
- In each step, the boat must carry 1 or 2 animals across the river.
- The boat must move during each step.
- The boat cannot move with zero animals inside.
- The wolves will eat the goats only if the wolves outnumber the goats on either side.
- All six animals must survive.
Here is a visualization (created in Forge) of one possible solution to this problem.
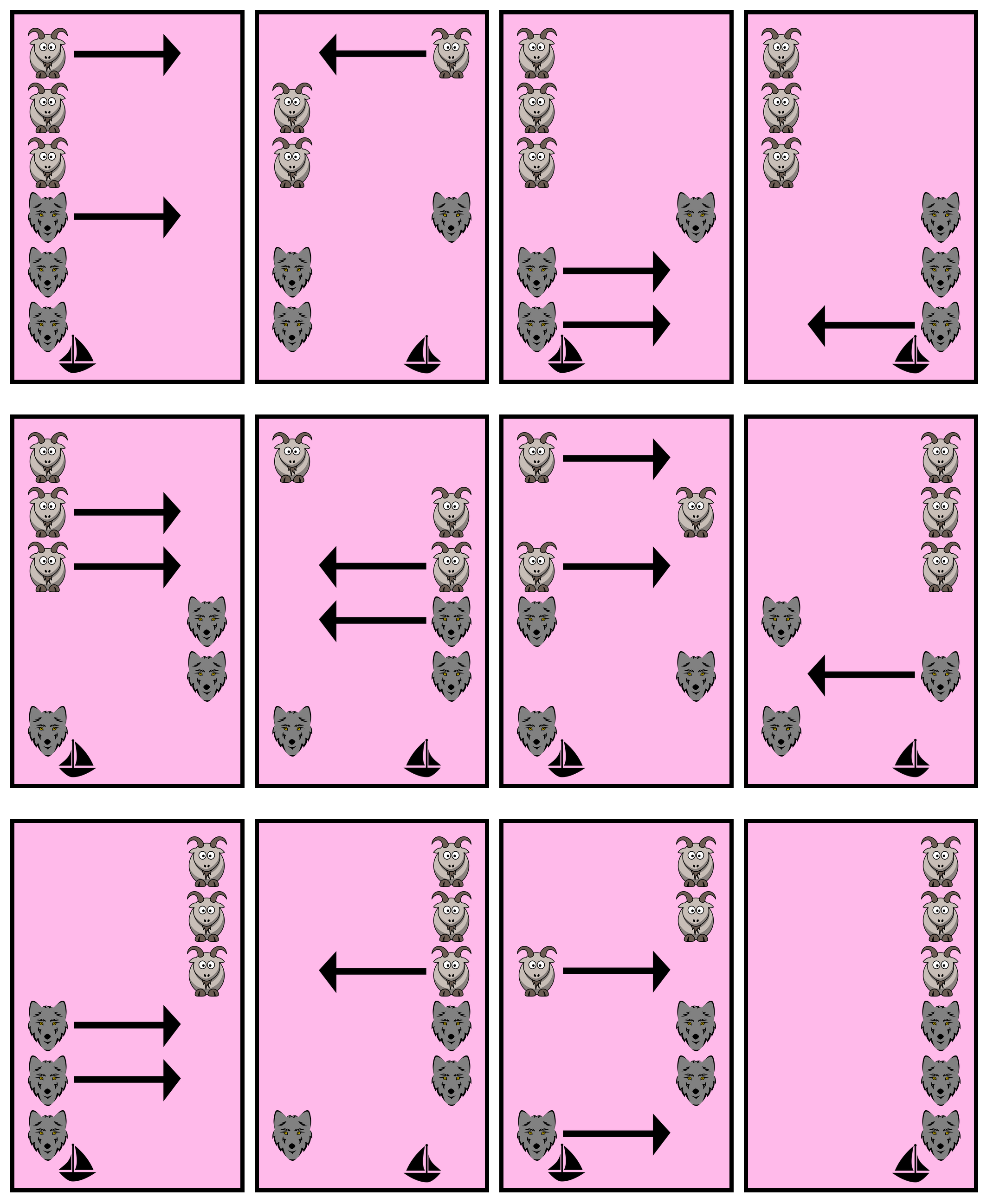
A Quick Diff
I wrote idiomatic models for the Goat-Wolf problem in Froglet and Temporal Forge. I diff’ed the two files on my computer, and three apparent differences popped out:
- In Froglet, the user must manage state explicitly, but Temporal Forge manages state implicitly
- Froglet requires the user to pass state signatures to each predicate, while Temporal Forge is able to elide this requirement
- The user must ‘explain’ how time works to Froglet
In regards to the first point, here are the relevant code snippets from each language and their significance:
#lang forge/froglet
abstract sig Animal {}
sig State {
next: lone State,
shore: pfunc Animal -> Position,
boat: one Position
}To handle state in Froglet, we declare a signature called State.
The shore field tracks our animals’ position by mapping from Animal to Position.
The last field, boat, stores the boat’s position.
The first field, next, may point to our next state (the lone keyword means at most one).
This is meant to create a ‘linked list’ of State signatures that track the positions of our entities over time (this alone won’t make a correct ‘linked list’ of time states; we must also declare linearity, which we rectify in the next section).
This is in stark contrast to the implicit expression of states in Temporal Forge:
#lang forge/temporal
abstract sig Animal { var p: one Position }
sig Boat { var p: one Position }Temporal Forge tracks state implicitly, hiding its internal representation from the user.
Because of this, Temporal Forge also allows its signatures to mark their fields as var.
Compared to Froglet’s always static fields, a var field denotes that the field’s value may change across states.
Regarding the second difference, the requirement to pass state signatures to each predicate in Froglet is a consequence of the abovementioned point. Froglet’s explicit state management requires the explicit passing of states to predicates.
#lang forge/froglet
pred initState[s: State] {
s.boat = Near
all a: Animal | { s.shore[a] = Near }
}
pred canTransition[pre: State, post: State] {
pre.boat != post.boat
...
}The initState predicate declares that the boat and the animals must start on the near shore.
In the Froglet example above, initState takes one parameter of type State.
It then inspects the state to ensure that all entities are indeed at the near shore.
The canTransition predicate enforces that transitions between states must be valid.
Shown above, is that transitions must follow the rule stating “the boat must move during each step.”
It does this by stating that the location of the boat must be different between the pre and post-states (all of the other rules regarding state transitions are encoded into this predicate but have been omitted for brevity).
Temporal Forge’s implicit state passing is ever so slightly more brief:
#lang forge/temporal
pred initState {
Boat.p = Near
all a: Animal | a.p = Near
}
pred canTransition {
Boat.p != Boat.p'
...
}Regarding initState, since each signature (boat and animal) now holds its location (the value of which can change over implicit time steps), there’s no state signature left to pass to the predicates.
For canTransition, Temporal Forge provides the prime operator (').
The prime operator makes an expression, Boat.p, refer to its value in the next state.
The third difference I observed about having to ‘explain’ time to Froglet:
#lang forge/froglet
pred TransitionStates {
some init, final: State {
initState[init]
finalState[final]
no s: State { s.next = init }
no s: State { final.next = s }
reachable[final, init, next]
all pre: State | all post: pre.next { canTransition[pre, post] }
}Froglet must use the TransitionStates predicate to constrain how the solver handles the time signature (Time must be linear and have a definite beginning and end).
In line 4 of the code snippet above, we declare that there must exist some pair of states, called init and final, which must satisfy the following conditions.
The init state must follow the initState predicate.
initState isn’t particularly interesting. It just states that the boat and all of the animals must begin on the near shore (as per the problem definition).
Ditto, for the final state, the animals and the boat must end up on the far side of the river.
Line 8 declares that no state may precede the initial state.
Line 9 is similar by specifying that no state may follow the final state.
On line 11, we use a special reachability relation created just for Froglet. Here, it defines that starting at init and following on to the next state, we must eventually reach final.
The final line in the TransitionStates predicate looks intimidating, so I’ll break it down.
It declares that for every state, ‘pre,’ and for every possible state, ‘post’ that could follow ‘pre,’ these two states must obey the canTransition predicate (canTransition is the same predicate referred to in the second difference).
Such as: “In each step, the boat must carry 1 or 2 animals across the river.” or “The boat must move during each step.” etc.
In much simpler terms, line 13 says, “Each transition between timesteps must follow the rules laid out in canTransition.”
Compare this to Temporal Forge’s timestep management:
#lang forge/temporal
{
initState
always { canTransition }
eventually finalState
}Temporal Forge has particular constructs for handling these events directly.
These constructs make it intuitive to see that the first state must follow the rules of initState.
During state transition, the rules of canTransition must always be applied.
Eventually, the model must end according to the finalState predicate.
Conclusion
If Temporal Forge has all this expressive power, why bother with the less expressive modes? I see three compelling reasons for a simpler language.
- Some modeling problems don’t require a time domain to be expressed, such as solving Sudoku
- Temporal Forge is a much more complex language than Froglet; starting with a simpler system is a better way to teach formal methods to students
- Although it didn’t come up in this comparison, Froglet is much nicer when the specification requires simultaneously referring to two or more states. It’s easy to keep a reference to any of Froglet’s time states, while the nature of Temporal Forge’s always-changing state can make it tricky to keep a handle on multiple states simultaneously.
More Resources
For those who find themselves interested in learning more about Forge,